IDEA INTUITIVA : La derivada mide el ritmo de cambio de una variable respecto de otra.
En nuestro caso analizamos la razón entre el incremento en el eje y, y el incremento en el eje x de diferentes puntos que pertenecen a una curva (Gráfica). Es decir, para subir una unidad en el eje y, necesitamos saber cuantas unidades se recorren en el eje x.
EJEMPLO N° 1:Dada la función f(x) = √x , hallar la razón del incremento entre el eje y y el eje x en el punto x = 1 .
PASO N°1: Dibujemos la gráfica de f(x), con ayuda de un graficador.
PASO N°2: Trazamos la recta tangente a f(x) en el punto de abscisa x = 1. (Línea roja).
PASO N°3: Observamos el triángulo delimitado por los segmentos que unen los siguientes punto:
- Punto de tangencia (Punto A)
- El punto de coordenadas ENTERAS por donde pasa la tangente y mas cercano al punto A (Punto B)
- El punto de intersección entre los segmentos perpendiculares que pasan por A y B. (Punto C)
Como podemos observar en la siguiente gráfica para ascender 1 unidad en el eje y debemos de recorrer 2 unidades en el eje x .
- Si denotamos por Δy, el incremento en la ordenada y.
- Y si denotamos por Δx, el incremento en la ordenada x.
Simbólicamente representamos esta razón de la siguiente manera:
Matemáticamente decimos que esta razón es la pendiente de la recta tangente a f(x) = √x en en el punto de abscisa x = 1 y simbólicamente representamos como:
EJEMPLO N° 2: UTILIZANDO EL SIGUIENTE APPLET.
Dada la función f(x) = √x , hallamos la pendiente de la recta tangente a f(x) en el punto de abscisa x = 4 .
EJEMPLO N° 3: UTILIZANDO EL SIGUIENTE APPLET.
Dada la función f(x) = √x , hallamos la pendiente de la recta tangente a f(x) en el punto de abscisa x = 9 .
NOTA
1. Si la recta tangente es CRECIENTE (Asciende de izquierda a derecha) la pendiente es POSITIVA.
2. Si la recta tangente es DECRECIENTE (Desciende de izquierda a derecha) la pendiente es NEGATIVA.
1 Hallar la pendiente de la recta tangente en el punto x = -2.

2 Hallar la pendiente de la recta tangente en el punto x = -1.

3 Hallar la pendiente de la recta tangente en el punto x = 2.

4 Hallar la pendiente de la recta tangente en el punto x = 0.

5 Hallar la pendiente de la recta tangente en el punto x = 0.

6 Hallar la pendiente de la recta tangente en el punto x = 0.

7 Hallar la pendiente de la recta tangente en el punto x = 1.
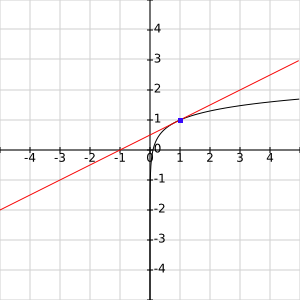
8 Hallar la pendiente de la recta tangente en el punto x = 1.

9 Hallar la pendiente de la recta tangente en el punto x = 0.

10 Hallar la pendiente de la recta tangente en el punto x = 0.

11 Hallar la pendiente de la recta tangente en el punto x = 1.

12 Hallar la pendiente de la recta tangente en el punto x = 2.







Pongan las respuestas de los ejercicos xd
ResponderBorrar