DEFINICIÓN:
EJEMPLOS:
TÉRMINO GENERAL DE UNA SUCESIÓN RACIONAL
donde bn y cn son sucesiones lineales o cuadráticas. y n es el número del término deseado.
CASO N° 1: El numerador es una constante y el denominador una sucesión lineal o cuadrática.
PASO N° 1: Hallamos el término general del numerador, o sea bn, está claro que bn = 1.
PASO N° 2: Hallamos el término general del denominador, o sea cn,
Verificamos si la sucesión cn, es lineal: an + b o es cuadrática an2 + bn + c

La diferencia en el Nivel 1 es una constante ( 1 ), por lo tanto la sucesión Cn = { 2, 3, 4, 5, 6, 7, . . . } es una sucesión LINEAL de la forma Cn = an + b.
Esta diferencia d = 1 será el valor de la constante a. → a = 1.
PASO N° 3: Hallamos el valor de la constante b,
Para encontrar el valor de b podemos utilizar el primer término, c1 = 2 en donde n = 1.
De esta forma:
c1 = a (1) + b → 2 = 1(1) + b, → b = 1.
PASO N° 4: La sucesión del numerador es:
Si a = 1 y b = 1 → cn = an + b → cn = n + 1.
Finalmente escribimos el cociente entre la sucesión del numerador y la sucesión del denominador.
EJERCICIOS RESUELTOS CAS0 N° 1:
CASO N° 2: El numerador es una sucesión lineal y el denominador una sucesión lineal o cuadrática.
PASO N° 1: Hallamos el término general del numerador, o sea bn,.
Verificamos si la sucesión bn, es lineal: an + b o es cuadrática an2 + bn + c

La diferencia en el Nivel 1 es una constante ( 3 ), por lo tanto la sucesión bn = { 0, 3, 6, 9, 12, 15, . . . } es una sucesión LINEAL de la forma bn = an + b.
Esta diferencia d = 3 será el valor de la constante a. → a = 3.
PASO N° 2: Hallamos el valor de la constante b,
Para encontrar el valor de b podemos utilizar el primer término, b1 = 0 en donde n = 1.
De esta forma:
b1 = a (n) + b → 0 = 3(1) + b, → b = -3.
PASO N° 3: La sucesión del numerador es:
Si a = 3 y b = -3 → bn = an + b → bn = 3n - 3.
..:: REPETIR LOS PASOS 1, 2 y 3 PARA EL DENOMINADOR ::..
PASO N° 4: Hallamos el término general del denominador, o sea cn,.
Verificamos si la sucesión cn, es lineal: an + b o es cuadrática an2 + bn + c

La diferencia en el Nivel 1 es una constante ( 3 ), por lo tanto la sucesión Cn = { -1, 2, 5, 8, 11, 14, . . . } es una sucesión LINEAL de la forma Cn = an + b.
Esta diferencia d = 3 será el valor de la constante a. → a = 3.
PASO N° 5: Hallamos el valor de la constante b,
Para encontrar el valor de b podemos utilizar el primer término, c1 = -1 en donde n = 1.
De esta forma:
c1 = a (n) + b → -1 = 3(1) + b, → b = - 4.
PASO N° 6: la sucesión del denominador es:
Si a = 3 y b = -4 → cn = an + b → cn = 3n - 4.
Finalmente escribimos el cociente entre la sucesión del numerador y la sucesión del denominador.
EJERCICIOS RESUELTOS CAS0 N° 2:
CASO N° 3: El numerador es lineal o cuadrática y el denominador es lineal o cuadrática.
PASO N° 1: Hallamos el término general del numerador, o sea bn,.
Verificamos si la sucesión bn, es lineal: an + b o es cuadrática an2 + bn + c

La diferencia en el Nivel 1 es una constante ( 1 ), por lo tanto la sucesión bn = { 0, 1, 2, 3, 4, 5, 6, . . . } es una sucesión LINEAL de la forma bn = an + b.
Esta diferencia d = 1 será el valor de la constante a. → a = 1.
PASO N° 2: Hallamos el valor de la constante b,
Para encontrar el valor de b podemos utilizar el primer término, b1 = 0 en donde n = 1.
De esta forma:
b1 = a (n) + b → 0 = 1(1) + b, → b = -1.
PASO N° 3: La sucesión del numerador es:
Si a = 1 y b = -1 → bn = an + b → bn = n - 1.
..:: REPETIR LOS PASOS 1, 2 y 3 PARA EL DENOMINADOR ::..
PASO N° 4: Hallamos el término general del denominador, o sea cn,.
Verificamos si la sucesión cn, es lineal: an + b o es cuadrática an2 + bn + c

La diferencia en el Nivel 2 es una constante ( 2 ), por lo tanto la sucesión cn = { 2, 5, 10, 17, 26, 37, 50, . . . } es una sucesión CUADRÁTICA de la forma cn = an2 + bn + c.
PASO N° 5: Para encontrar el valor de a, b, c podemos utilizar el método de las diferencias.
Ahora establezcamos las siguientes relaciones:
Primer término de la sucesión = a1 → a1 = a + b + c = 2.
Primer término de la diferencia del Nivel 1 = d0 → d1 = 3a + b = 3,
Primer término de la diferencia del Nivel 2 = D0 → D0 = 2a = 2,
Para finalizar resolvemos las siguientes ecuaciones:
Por lo tanto el término general de la sucesión será: an2 + bn + c = 1n2 + 0n + 1 = n2 + 1
Finalmente escribimos el cociente entre la sucesión del numerador y la sucesión del denominador.
EJERCICIOS PROPUESTOS
Hallar el término general en las siguientes sucesiones racionales:










Se llama término general de una sucesión, y se simboliza con an, a la expresión que representa uno cualquiera de sus términos.
Hay sucesiones cuyo término general es una expresión algebraica, que nos permite saber cualquier término de la sucesión sabiendo el lugar que ocupa, n.EJEMPLOS:

|

|

|

|
| El término general de una sucesión racional es de la forma: | con |
| NOTA: En este apartado solo trataremos sucesiones racionales que involucran sucesiones lineales y / o sucesiones cuadráticas, las demás sucesiones de orden superior no serán tenidas en cuenta. |
En este tipo de sucesiones racionales tratamos por separado el numerador y el denominador, como si fueran dos sucesiones diferentes.
Pueden resultar tres (3) tipos diferentes de sucesiones racionales según los siguientes casos:CASO N° 1: El numerador es una constante y el denominador una sucesión lineal o cuadrática.
| EJEMPLOS: Hallar el término general de la siguiente sucesión |

|
PASO N° 2: Hallamos el término general del denominador, o sea cn,
Verificamos si la sucesión cn, es lineal: an + b o es cuadrática an2 + bn + c
- Una sucesión es lineal, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 1)
- Una sucesión es Cuadrática, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 2)

La diferencia en el Nivel 1 es una constante ( 1 ), por lo tanto la sucesión Cn = { 2, 3, 4, 5, 6, 7, . . . } es una sucesión LINEAL de la forma Cn = an + b.
PASO N° 3: Hallamos el valor de la constante b,
Para encontrar el valor de b podemos utilizar el primer término, c1 = 2 en donde n = 1.
De esta forma:
c1 = a (1) + b → 2 = 1(1) + b, → b = 1.
PASO N° 4: La sucesión del numerador es:
Si a = 1 y b = 1 → cn = an + b → cn = n + 1.
Finalmente escribimos el cociente entre la sucesión del numerador y la sucesión del denominador.
| Entonces | → |

|
→ |

|
CASO N° 2: El numerador es una sucesión lineal y el denominador una sucesión lineal o cuadrática.
| EJEMPLOS: Hallar el término general de la siguiente sucesión |

|
Verificamos si la sucesión bn, es lineal: an + b o es cuadrática an2 + bn + c
- Una sucesión es lineal, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 1)
- Una sucesión es Cuadrática, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 2)

La diferencia en el Nivel 1 es una constante ( 3 ), por lo tanto la sucesión bn = { 0, 3, 6, 9, 12, 15, . . . } es una sucesión LINEAL de la forma bn = an + b.
PASO N° 2: Hallamos el valor de la constante b,
Para encontrar el valor de b podemos utilizar el primer término, b1 = 0 en donde n = 1.
De esta forma:
b1 = a (n) + b → 0 = 3(1) + b, → b = -3.
PASO N° 3: La sucesión del numerador es:
Si a = 3 y b = -3 → bn = an + b → bn = 3n - 3.
PASO N° 4: Hallamos el término general del denominador, o sea cn,.
Verificamos si la sucesión cn, es lineal: an + b o es cuadrática an2 + bn + c
- Una sucesión es lineal, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 1)
- Una sucesión es Cuadrática, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 2)

La diferencia en el Nivel 1 es una constante ( 3 ), por lo tanto la sucesión Cn = { -1, 2, 5, 8, 11, 14, . . . } es una sucesión LINEAL de la forma Cn = an + b.
PASO N° 5: Hallamos el valor de la constante b,
Para encontrar el valor de b podemos utilizar el primer término, c1 = -1 en donde n = 1.
De esta forma:
c1 = a (n) + b → -1 = 3(1) + b, → b = - 4.
PASO N° 6: la sucesión del denominador es:
Si a = 3 y b = -4 → cn = an + b → cn = 3n - 4.
Finalmente escribimos el cociente entre la sucesión del numerador y la sucesión del denominador.
| Entonces | → |

|
→ |
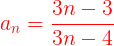
|
CASO N° 3: El numerador es lineal o cuadrática y el denominador es lineal o cuadrática.
| EJEMPLOS: Hallar el término general de la siguiente sucesión |
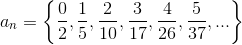
|
Verificamos si la sucesión bn, es lineal: an + b o es cuadrática an2 + bn + c
- Una sucesión es lineal, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 1)
- Una sucesión es Cuadrática, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 2)

La diferencia en el Nivel 1 es una constante ( 1 ), por lo tanto la sucesión bn = { 0, 1, 2, 3, 4, 5, 6, . . . } es una sucesión LINEAL de la forma bn = an + b.
PASO N° 2: Hallamos el valor de la constante b,
Para encontrar el valor de b podemos utilizar el primer término, b1 = 0 en donde n = 1.
De esta forma:
b1 = a (n) + b → 0 = 1(1) + b, → b = -1.
PASO N° 3: La sucesión del numerador es:
Si a = 1 y b = -1 → bn = an + b → bn = n - 1.
PASO N° 4: Hallamos el término general del denominador, o sea cn,.
Verificamos si la sucesión cn, es lineal: an + b o es cuadrática an2 + bn + c
- Una sucesión es lineal, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 1)
- Una sucesión es Cuadrática, si la diferencia entre dos términos consecutivos cualesquiera es un CONSTANTE (NIVEL 2)

La diferencia en el Nivel 2 es una constante ( 2 ), por lo tanto la sucesión cn = { 2, 5, 10, 17, 26, 37, 50, . . . } es una sucesión CUADRÁTICA de la forma cn = an2 + bn + c.
PASO N° 5: Para encontrar el valor de a, b, c podemos utilizar el método de las diferencias.
Ahora establezcamos las siguientes relaciones:
Primer término de la sucesión = a1 → a1 = a + b + c = 2.
Primer término de la diferencia del Nivel 1 = d0 → d1 = 3a + b = 3,
Primer término de la diferencia del Nivel 2 = D0 → D0 = 2a = 2,
Para finalizar resolvemos las siguientes ecuaciones:
Por lo tanto el término general de la sucesión será: an2 + bn + c = 1n2 + 0n + 1 = n2 + 1
Finalmente escribimos el cociente entre la sucesión del numerador y la sucesión del denominador.
| Entonces | → |

|
→ |
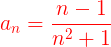
|
Hallar el término general en las siguientes sucesiones racionales:













No hay comentarios.:
Publicar un comentario