DEFINICIÓN:
La función especial por tramos corresponde a funciones que están definidas por diferentes funciones reales en distintas partes de su dominio. Para trazar su gráfica bastará con construir cada una en un mismo plano, pero solamente la parte correspondiente al intervalo indicado.
EJEMPLO DE LA FUNCIÓN POR TRAMOS:
| FUNCIÓN: |
GRÁFICA |

|

|
La gráfica anterior es una función por tramos que está conformada por tres (3) funciones Reales, asi:
| TRAMO N° 1: |
TRAMO N° 2: |
TRAMO N° 3: |
| FUNCIÓN CONSTANTE |
FUNCIÓN CUADRÁTICA |
FUNCIÓN LINEAL |
| f(x) = 3 |
f(x) = x2 - 1 |
f(x) = x + 1 |
CARACTERÍSTICAS Y PASOS PARA GRAFICAR LA FUNCIÓN POR TRAMOS:
Las gráficas de las función por partes no son difíciles de dibujar, pero es necesario tener en cuenta algunos aspectos importantes. Para dibujar una gráfica de esta función se debe tener en cuenta los siguientes aspectos:
EJEMPLO N ° 1
| Dada la función |

|
graficar aplicando los siguiente pasos: |
1. Elaborar una tabla de datos: Analicemos cada tramo:
TRAMO N° 1 : la función
x2 →
FUNCIÓN CUADRÁTICA., → para valores de
x < 2 .
|
X
|
-2
|
-1
|
0
|
1
|
2
|
|
Y
|
4
|
1
|
0
|
1
|
4
|
OJO: En x = 2 NO ESTA DEFINIDA, pero cuando se acerca a 2 por la izquierda, la función se aproxima a 4.
TRAMO N° 2 : la función
4 →
FUNCIÓN CONSTANTE., → para valores de
x > 2 .
OJO: En x = 2 NO ESTA DEFINIDA, pero cuando se acerca a 2 por la izquierda, la función se aproxima a 4.
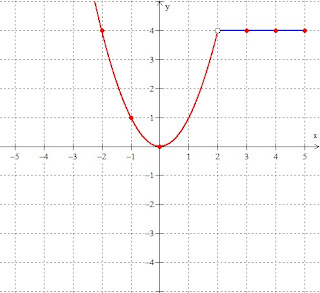
2. Representar cada punto en el plano:
En x = 2, LA FUNCIÓN NO ESTA DEFINIDA, NO EXISTE GRÁFICA, APARECE UN HUECO.
3.
Dominio: El dominio de la función son todos los reales menos el 2,
R - {2} → Df: (-∞, 2) U (2, ∞)
4. Rango: El rango de la función son todos los reales mayores o iguales a 0,
R+ → Rf: (0, ∞)
EJEMPLO N ° 2
| Dada la función |

|
graficar aplicando los siguiente pasos: |
1. Elaborar una tabla de datos: Analicemos cada tramo:
TRAMO N° 1 : la función
x2 + 2x →
FUNCIÓN CUADRÁTICA., → para valores de
x < -1 .
TRAMO N° 2 : la función
x →
FUNCIÓN LINEAL., → para valores de
- 1 < x < 1 .
OJO: En x = -1 y x = 1 NO ESTA DEFINIDA, pero cuando se acerca a - 1 por la derecha, la función se aproxima a -1. y cuando se acerca a 1 por la izquierda, la función se aproxima a 1.
TRAMO N° 3 : la función
-2x + 3 →
FUNCIÓN EXPONENCIAL., → para valores de
x < 1 .
2. Representar cada punto en el plano:
3. Dominio: El dominio de la función son todos los reales,
R → Df: (-∞, ∞)
4. Rango: El rango de la función son todos los reales,
R → Rf: (-∞, ∞)
EJERCICIOS RESUELTOS
EJERCICIOS PROPUESTOS
|
1.
|

|
|
2.
|

|
|
3.
|

|
|
4.
|

|
|
5.
|

|
|
6.
|

|
|
7.
|

|
|
8.
|

|
|
9.
|

|
|
10.
|
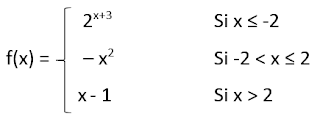
|















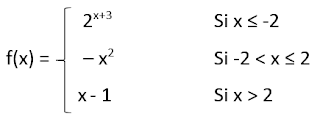


Buenos e interesantes ejercicios.
ResponderBorrarMuchas gracias
Mis dos Secciones han sido remitidas a está página...para estudar los ejemplos y realizar el taller propuesto. Gracias estimado profesor.
ResponderBorrarHola, quería saber cómo encontrar la resolución de los ejercicios propuestos para comparar con mis resultados gracias
ResponderBorrarHay una página de Solucionarios de Matemáticas que te puede interesar
ResponderBorrarNo entendí ni pja
ResponderBorrar