Las derivadas de orden superior se obtienen al derivar una función y = f (x), tantas veces como lo indique el orden requerido.
|

|
|

|
- El proceso de hallar derivadas, una tras otra, se llama derivadas sucesivas.
|

|
Si derivamos la derivada de una función, derivada primera, obtenemos una nueva función que se llama derivada segunda, f ' '(x). Si volvemos a derivar obtenemos la derivada tercera, f ' ' '(x). Si derivamos otra vez obtenemos la cuarta derivada f ' ' ' ' y así sucesivamente.
EJEMPLO N° 1
Obtenga la Tercera derivada de la función f(x) = 2x3 + 4x2 – 5x + 1
PASO N° 1
| Se obtiene la primera derivada de la función: |

|
PASO N° 2
| Se obtiene la segunda derivada de la función: |

|
PASO N° 3
| Se obtiene la segunda derivada de la función: |

|
EJEMPLO N° 2
| Obtenga la segunda derivada de la función |

|
PASO N° 1
| Se obtiene la primera derivada de la función: |

|
PASO N° 2
| Se obtiene la segunda derivada de la función: |

|
EJEMPLO N° 3
| Obtenga la segunda derivada de la función |

|
PASO N° 1
| Se obtiene la primera derivada de la función: |

|
PASO N° 2
| Se obtiene la segunda derivada de la función: |

|
EJEMPLO N° 1
EJEMPLO N° 1
Obtenga la segunda derivada de la función











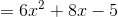




















ayudeme con este ejercicio de 2da derivada
ResponderBorrarf(x)=4/(x^2+2)
Alguien me puede ayudar co unos ejercicios y= 3x/lnx
ResponderBorrarAlguien me puede hacer el favor de ayudar con unos ejercicios f(x)=8 derivada de orden superior
ResponderBorrarSería F'(x)= 0
Borrar